Commercially available pulsation analysis software uses either a transient (time domain) or harmonic (frequency domain) solver. A time domain solver is more accurate for determining the pulsation amplitude, but solving in the frequency domain can be orders of magnitude faster. Which solver should you use and why is there a difference? In this post the two methods are compared for a pulsation bottle of a reciprocating compressor.
First let us review why there is a difference
The simplified 1-D wave equations for motion and continuity are shown below. These are solved by both the time and frequency domain solvers. Here attention is directed to the term in red, this is the dampening term where f is the friction factor, D is the pipe diameter and V is the velocity.
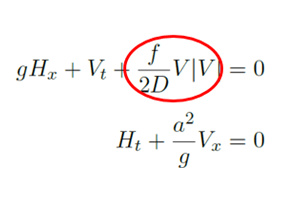
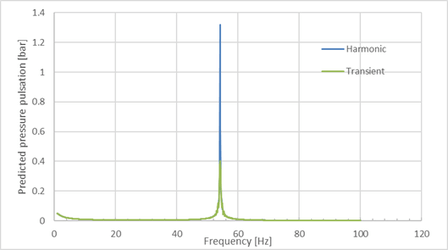
In the time domain solver, the term V and |V| are approximated by using the calculated velocity together with the velocity at the previous time step. This is a good representation of the frictional dampening which is proportional to velocity squared. In the harmonic solver, the solution is obtained in the frequency domain (using a Fourier transform). Therefore, a different approximation of the V|V| term is needed. In many solvers, V is the steady state velocity and |V| is the perturbation velocity. This means that if the steady velocity is low compared to the perturbation velocity (large pulsation amplitude) then dampening is under-predicted. This is especially relevant for dead end branches, where the velocity is zero in the steady state. It should be noted that simply ignoring the pulsations in the dead end branch does not remove the inaccuracy, as excited acoustical modes extend through the entire piping network. As a result, predicted pulsations using the harmonic solver can be several times larger than those using the transient solver. This is shown in figure 1 for a typical inline pulsation bottle for a liquid system, analyzed using both the harmonic and the transient solution method. It can be noted that, away from the location of resonance, both solution methods predict almost identical pulsations amplitudes. Near the location of resonance at which the flow fluctuations become large, the difference can become large. Although this example shows the over-prediction of pulsation amplitudes using the harmonic solver, more complex cases can result in an under-prediction of pulsations using the harmonic solver. This is especially relevant for using acoustic resonance at one part of the system to dampen pulsations at another part (for example side-branch resonance).
What is the effect for a pulsation bottle?
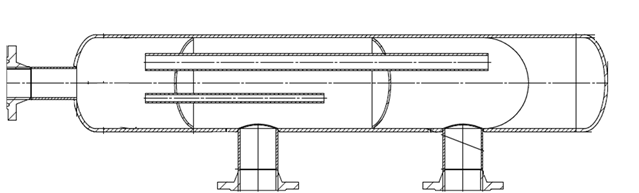
As shown above, for some cases with large pulsation amplitudes the difference between harmonic and time-domain can be very significant. However, in practice the difference may not be so extreme. A typical pulsation bottle is shown in figure 2.
Pulsation amplitudes at the piping/flange nozzle are shown for the two solvers in figure 3 as computed using the different solution methods. From figure 3 it can be seen that the calculated acoustical resonance frequencies are the same for both the two solution methods. The harmonic solver predicts a 20% higher pulsation amplitude near the resonance frequency.

So which solver to use?
Often the difference in pulsation amplitude between the harmonic and time domain is small but not negligible. Therefore, if both solvers are available the harmonic solver can be employed for initial design purposes using fast sweeps of different configurations, as the calculated resonance frequency is the same for both time and frequency domain solvers. As soon as a feasible solution is obtained, the final design can be simulated using the transient solver only once to accurately validate the design.
All simulations and results were obtained using the commercially available software BOSpulse. The software is validated and developed using several decades of engineering consulting services as conducted by DRG. The software includes both solutions methods, harmonic and transient, in a single module.
Curious or need more information: